2進数の小数表現
2進数の小数
10進数と同じように、2進数でも小数点以下の数、つまり小数をあつかうことが可能です。また、2進数同様に循環小数などといった概念も存在します。ここでは、2進数で小数を表現した場合、それを10進数で表した場合にどうなるか、そして逆に10進数の小数を2進数に変換するにはどうしたらよいかといったようなことについて学習します。
2進数から10進数の変換
2進数の小数から10進数の小数への変換
2進数から10進数への変換方法は、整数部と小数部では基本的に同じ方法で、2進数の各けたの数値とけたの重みをかけたものと合計を計算することにより求められます。桁の重み付けは、小数点を起点にして整数の場合は右から左に20、21、22…、であったのに対し、小数部は左から右に2-1、2-2、2-3…と各けたに重み付けをおこないます。(図4-1.)
図4-1.2進数の桁の重みづけ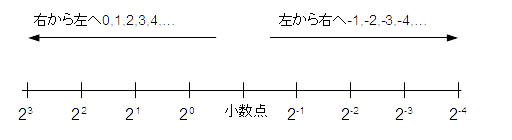
なので、例えば2進数で0.101と表現した場合は、10進数での表現は以下のようになります。(図4-2.)
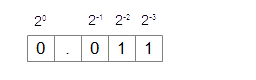
となります。2進数の0.101は、10進数では0.625であることがわかります。
整数部分がある場合
続いて、整数部分もある小数について考えてみましょう。2進数の101.011を10進数に変換してみます。すると
= 1×4 + 0×2 + 1×1 + 0×0.5 + 1 × 0.25 + 1× 0.125
= 4 + 1 + 0.25 + 0.125 = 5.275
となり、10進数では5.275となることがわかります。(図4-3.)
図4-3.2進数の小数の表現②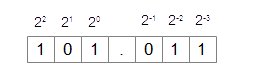
2進数から10進数への変換
10進数の小数を2進数に変換する
続いて、10進数の小数を2進数に変換する方法をみてみましょう。すでに説明したとおり、2進数の小数は、以下のような形で表現されています。(図4-3.)
図4-4.2進数の小数の一般的な表現方法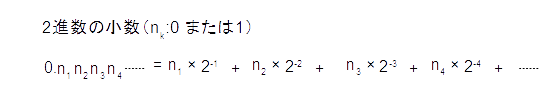
n
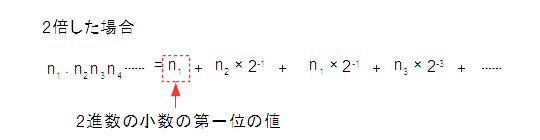
すると、元の数の小数の第一位の数値のみが整数になることがわかります。このn1をこの値から取り除き、さらに同じ子をと繰り返すことにより、n2、n3…といった値が得られることがわかります。10進数を2進数に変換するには、この方法を応用します。では、実際に小数10進数の0.625を2進数に変換してみましょう。
では実際に、10進数0.625を2進数に変換してみましょう。まずはこの値を2倍すると、1.25になります。ここから、1の位の1を取り除いた0.25にさらに2をかけ、ということをくりかえします。そして、値が1.0になったところで計算は終了します。(図4-6.)
図4-6.10進数の小数を2進数に変換①
循環小数
続いて、小数0.2を10進数に変換してみましょう。今度は、値に2をかけ、1の位を取り除くという作業を繰り返していくと、また元の値の0.2に戻ってしまいます。
図4-7.10進数の小数を2進数に変換②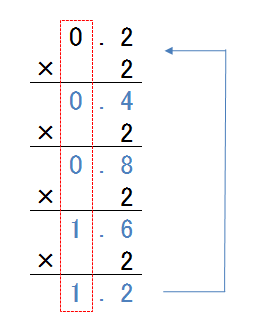
通常は、値が1.0になれば計算は終了ですが、この場合は計算が終わらず、0.00110011…と、「0011」が繰り返されるような値になります。
このように、小数点以下の数が無限に続く小数のことを、無限小数と言い、さらにそこで同じパターンが繰り返し出現する場合を循環小数と言います。無限小数に対して、小数部が0になるものを有限小数と言います。
無限小数が発生した場合は、コンピューターの内部では数値の近似値で数値を表す必要があり、そのための方法は様々な方法があります。









