論理演算
2進数による論理演算
続いては、2進数による論理演算について説明します。論理演算は、加減乗除のような算術演算以外の種類の演算ですが、コンピュータがもっとも得意とする計算です。実は、算術演算ですらこの論理演算の組み合わせでできているのです。
論理演算には,AND,OR,XOR,NOTの4種類があります。論理演算と四則演算の大きな違いは,論理演算が2進数の1けた(=1ビット)を対象としていること、そして演算結果のけた上がりがないことです。ここでは2進数による論理演算と、その応用について説明します。
論理演算の種類
論理積
では実際に、2進数による論理演算を見てみましょう。まずは、論理積(AND)から見ていきます。二進数による論理積の演算は、以下のようになります。(表6-1)
表6-1.論理積| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
AND演算(アンドえんざん)の機能は,英語のANDの意味そのもので,、「かつ」という意味です。そのため、1と1のAND演算結果だけが1になります。つまり演算する2つの値の両方が1なら演算結果が1になるのです。これは、掛け算の性質と大変似ているため、論理積と呼ばれます。
では、実際に8ビットの論理積の例を見てみましょう。01101101と、11110000のAND演算を行ってみます。複数の桁がある場合は、対応けた同士でそれぞれAND演算を行います。その結果、得られる答えは01100000となります。(図6-1.)
図6-1.8ビットのAND演算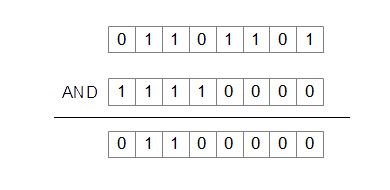
この演算で上位4ビットはもとの値のままです。これによって,データの上位4ビットだけを取り出せたことになります。11110000のように、任意のビットを0にクリアするために使われるデータのことをマスク・パターンと呼びます。マスク(mask)とは,覆い隠すという意味で、この演算結果のように、とくていのビットを覆い隠したいときに用いられます。
論理和
続いて2進数による論理和(OR)を見てみましょう。二進数による論理和の演算は、以下のようになります。(表6-2.)
表6-2.論理和| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
OR演算(オアえんざん)の機能は,英語のORの意味そのもので,、「~か」という意味です。そのため、OR演算結果では、二つのうち1つのどちらかが1であれば、答えは1になります。これは、足し算の性質と大変似ているため、論理和と呼ばれます。ただ、実際の足し算と違うのは、両方が「1」でも、桁上がりが起きないということです。
では、実際に8ビットの論理和の例を見てみましょう。ANDの場合と同様に、01101101と、11110000のOR演算を行ってみます。複数の桁がある場合は、対応けた同士でそれぞれOR演算を行います。その結果、得られる答えは11111101となります。(図6-2.)
図6-2.8ビットのOR演算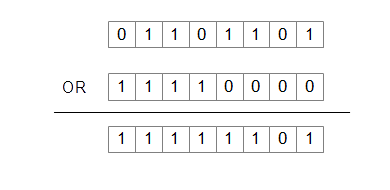
排他的論理和
次は2進数による排他的論理和(XOR)を見てみましょう。排他的論理和の演算は、以下のようになります。(表6-3.)
表6-3.排他的論理和| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
排他的論理和(XOR)と論理和(OR)の違いは、両方が「1」の場合は「0」になるということです。つまり、XOR演算は、どちらか一方だけが1の場合だけ1になるということになります。
では、実際に8ビットの排他的論理和の例を見てみましょう。ORの場合と同様に、01101101と、11110000のOR演算を行ってみます。複数の桁がある場合は、対応けた同士でそれぞれOR演算を行います。その結果、得られる答えは10011101となります。(図6-1.)
図6-3.8ビットのXOR演算
XOR演算では、1と演算する桁だけが反転し、0と演算する桁は変化しません。部分的な反転ができるのですXOR演算は、画像の特定の領域での画像のネガ・ポジ変換などのように、画像処理でよく使われます。
否定演算
最後に2進数による否定(NOT)を見てみましょう。この演算は非常に単純で、0と1をひっくり返すだけです。(表6-4.)
表6-4.否定演算| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
では、実際に8ビットの否定の例を見てみましょう。01101101に否定演算をすると、その結果得られる答えは10010010となります。(図6-4.)
図6-4.8ビットのNOT演算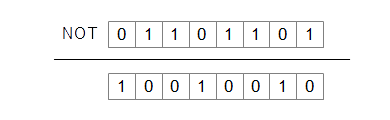
NOT演算は、算術演算で符号付きの整数の符号を逆転する際に、補数を求めるときの「反転して1」の「反転」のためなどに使われます。
その他
また、この他に、否定論理積(NAND)やと否定論理和(NOR)いったものがあります。これらは、それぞれ論理積や論理和の結果を逆転させたもので、それぞれの回路にNOT演算を行ったものです。ここでは、その内容を表で紹介するのにとどめておきます。(表6-5.表6-6.)
表6-5.否定論理積| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
表6-6.否定論理和
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
ド・モルガンの法則
正論値と負論理
実は、AND演算をOR演算で表現したり、逆にOR演算をAND演算で表現することもできます。一見不思議な感じがしますが、実際にそのことを証明するために、まずOR演算の1と0を逆転した表を見てみましょう。(表6-7.)
表6-7.OR演算の0と1を逆転させたもの| A | B | 結果 |
|---|---|---|
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 0 |
結果から明らかなように、これはまさしくAND演算です。今度は逆に、AND演算の0と1を逆転させたものを見てましょう。(表6-6.)
表6-5.AND演算の0と1を逆転させてもの| A | B | A AND B |
|---|---|---|
| 1 | 1 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 0 |
こちらもやはり、OR演算と同じものになることが分かります。一般に「真」を1,「偽」を0とすることを正論理と言い,逆に「真」を0,「偽」を1とすることを負論理と呼びます。つまり、表6-5.6-6.は負論理のOR,AND演算の結果の表なのです。
ド・モルガンの法則
正論理と負論理の結果化から、以下の法則が成り立つことが分かります。れを、ド・モルガンの法則と言います。ここでは,「・」でAND演算,「+」でOR演算,上付きの「 ̄」でNOT演算を表しています。(図6-5.)
図6-5.ド・モルガンの法則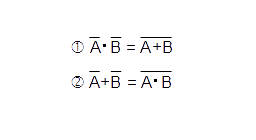
ド・モルガンの法則とは,AND演算で表された式とOR演算で表された式を相互に変換する方法を示したものです。









