バケットソート
バケットソートとは
ここでは、バケットソートというソートについて説明します。バケット(bucket)とは、英語でバケツという意味です。なぜバケツという言葉なのかということは、アルゴリズムを見れば明らかです。
たとえば、1から10の数のソートをするとします。そのとき、1から10の番号が入った「バケツ」を用意します。用意する数は、重複が合ってもかまいません。また、バケツには、複数の値を入れることができるとします。たとえば、2という値が重複すれば、2の値の入るバケツには、2が二つ入ります。 後の手順は簡単です。
あとは、数値を、値の該当する「バケツ」に入れます。すると、空っぽになっているバケツを除いて、順に値を取り出していけば、その値は自然に並べ替えられています。(図6-1.参照)
図6-1.バケットソートの構造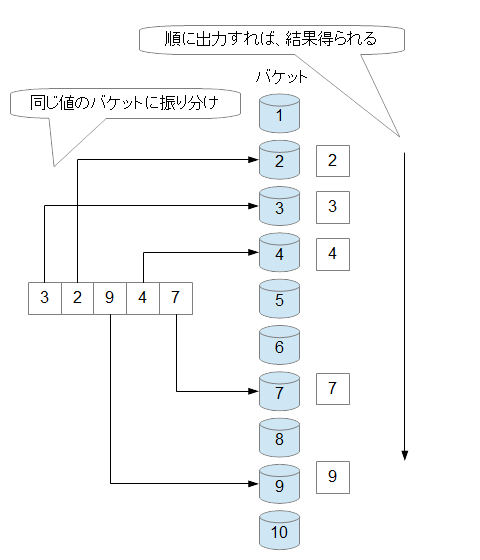
バケットソートの特徴
バケットソートの特徴は、なんといってもそのシンプルさです。データの数が10なら、10回、100なら100回のデータの処理をするだけでできてします、非常にシンプルで高速なアルゴリズムだといえます。
しかし、このアルゴリズムの問題点は、大量のメモリを必要とする点です。最低でも、ソートしたいデータの数だけのバケットを用意する必要があります。また、すべてのデータが重複する可能性もありますから、バケットには全データが入るだけの容量が必要になります。
具体的に説明すると、1から100までの数値を10個、並べ替えようとすると、バケツが、100個、さらに、そこに10個のデータが入るようにしなくてはなりませんから、配列を利用して実装しようと思ったら、100×10=1000個分のメモリが必要になります。
分布数え上げソート
分布数え上げソート
分布数え上げソートは、バケットソートをベースとしたソートアルゴリズムの一種です。並べ替えの対象となるデータをキーとし、キーの出現回数とその累積度数分布を計算して利用することで整列を行うアルゴリズムです。
バケットソートとの共通点は、データがとりうる値の範囲をあらかじめ知っている必要があるという点にあります。違いは、キーの重複に対応したアルゴリズムであるということです。
分布数え上げソートの手順
では、実際に、1から10までの数値の並べ替えのケースをもとに、分布数え上げソートの手順をみてみましょう。
- 並べ替えるデータ(値)の範囲に対応するバケットを用意する。
- キーと一致するデータの出現回数を数える。
- 入れ物の先頭から、キーをデータにして出現回数だけ取り出す。
分布数え上げソートの特徴
分布数え上げソートは、バケットソートと同様に、ソート対象のデータがとりうる値の範囲があらかじめわかっている必要があります。更にキーの個数をカウントする領域や、結果を格納する領域も必要になることから、大量の範囲のデータを取り扱うとメモリを圧迫してしまいます。しかし、データの大小を比較しなくてよいので処理は高速だというメリットがあります。
基数ソート
基数ソートとは
基数(きすう)ソートは、バケットソートを応用したソートです。基数とは、数を表現する際に、それぞれの桁をあらわす数です。たとえば、321という整数の場合、100の位は3、10の位は2、1の位は1という基数を持ちます。
基数ソートとは、この基数を用いたソートです。以下、3桁の整数の値を想定して、説明します。
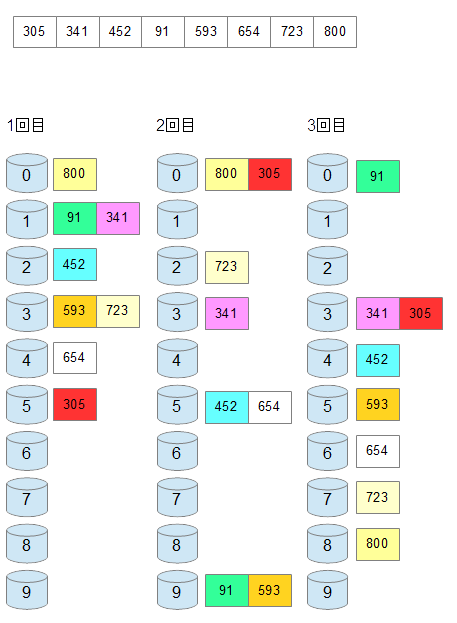
基数ソートの手順
前提として、0から9までのバケットを用意します。これは、基数が入るバケツです。以下、手順を説明します。
- 数値を、1の位の基数に分類すします。たとえば、101ならば、一の位の基数が1なので、1のバケツ、204なら、4なので、4の位に入れます。
- 次に、10の位の基数に着目し、すでに分類したものを、上のバケツに入っているデータから順にさらに該当するバケツに再分配します。たとえば、101は1のバケツから、0のバケツに移す。
- 最後に、100の位でも、同様の処理をします。この処理が終了すると、データは自然にならびかえられています。
基数ソートの特徴
基数ソートは、バケットソートの発展形であることから、基数ソートと同様の特徴を持ちます。ただ、バケットはあくまでも基数の分だけなので、メモリ数は基数ソートよりも少なくてすみます。
ただ、かわりに、計算回数は、基数ソートよりも、桁数分大きくなります。1から100までの数が10個の場合、バケットソートであれば、10回の処理、100個のバケツを必要としますが、基数ソートであれば、バケツは10個で済む代わりに、3回の計算を必要とします。
図6-2.ク基数ソートの構造