アルゴリズムと計算量
計算量とは
このサイトでは、さまざまなアルゴリズムを紹介してきましたが、こういったアルゴリズムの性能は、どのように評価すればよいのでしょうか?そもそも、アルゴリズムは、かかった時間で評価することは困難です。なぜなら、同じアルゴリズムで記述されたプログラムでも、実行環境やハードの性能が違えば、まるで違った結果になってしまうからです。
そのため、アルゴリズムの性能を評価するために、計算量(けいさんりょう)という指標が用いられます。計算量には、時間計算量と空間計算量とがあります。 前者は処理時間がどれだけ掛かるのかを表し、後者はどれだけの記憶容量を必要とするかを表します。 多くの場合、単に計算量と言えば、前者の時間計算量のことを指します。
O(オーダー)記法
前述のように、計算量とは、単純に「3秒かかる」といったような表現をしません。 そもそも「3秒」というのは、ある特定のハードの上での結果に過ぎず、他の環境で試せば値は変動してしまいますから、 性能評価の方法として不適切です。 そこで、その単位として、時間のようなものは用いず、「命令数(ステップ数)」を基準とします。なぜなら、1つの命令を実行するための時間は環境によって異なっても、同じ言語で同じように実装されたアルゴリズムの命令数は変わらないからです。
計算量の記述には、O記法(オーきほう、オーダーきほう)という表記が用いられるのが一般的です。 この「O」はオーダー(Order)という単語に由来し、ランダウの記号などとも呼ばれ、実行されるアルゴリズムが、どれほどの時間、記憶領域を使用するかを評価するも基準として用いられます。
例えば、O(n) のように記述し、この場合、データの個数 n に比例した時間が掛かることを表します。 よく登場するパターンは次の通りです。(表1-1.)
表1-1.代表的なオーダー| 記法 | 詳細 |
|---|---|
| O(n) | 命令数がデータ数に比例することを意味します。たとえば、2*nや、3*nといった計算量です。具体的には、n回、もしくは、nに比例する回数以内のループの処理で終わる場合がこれに該当すします。 |
| O(1) | 命令数がデータ数に比例することを意味します。たとえば、2*nや、3*nといった計算量です。 |
| O(n2) | このようなケースは少々複雑です。たとえば、2*n2 + 3*n + 1という計算量があったとします。この場合、 最大次数をとる、2*n2に着目し、O(n2)と表記します。O(n3)、O(n4)といった、より高次のものも同様です。 |
| O(log n) | データ数nとするとき、2をステップ数乗した値の定数倍が計算量になるようなアルゴリズムです。二分木などが、典型的な例です。 |
| O(nlog n) | マージソートのように、二分木のようにデータを分割し、かつそれらのデータ全体をリニアサーチするようなアルゴリズムの計算量です。二分木のオーダー(logn)×リニアサーチのオーダー(n)をかけあわせ、nlognとなります。 |
二分木探索のオーダー
ここでは、二分木検索の例で、計算量について説明しましょう。二分木検索は、データ全体をに分割しながら行うサーチです。そのため、データとステップ数の関連を表にすると、以下のよう(表1-2.)のようになります。
表1-2.データの量と二分木のステップ数の対応表| データの大きさ | ステップ数 |
|---|---|
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
この表からわかるとおり、n = 2^(ステップ数) が成り立つので、両辺 log をとると log n = (ステップ数) となります。 つまり、2分探索の時間計算量は O(log n) です。
計算量の応用
計算量からわかること
計算量を用いることのメリットは、処理時間にある程度の予測が立つことにあります。たとえば、O(n) のアルゴリズムでは、データの個数n が 2倍になれば、処理時間も 2倍になるであることがわかります。 ここで n が幾つなのかも、処理時間が何秒なのかも全く登場しないため、 特定のマシンや環境に依存せずに、アルゴリズムの性能が評価できます。(表1-3.)
表1-3.オーダーと代表的な計算量| 表記 | 意味 | 例 |
|---|---|---|
| O(1) | 定数 | 配列を添字アクセスする場合(ex. a[0] = 1;) |
| O(logn) | 対数 | 二分探索 |
| O(n) | 一時 | 線形探索 |
| O(nlog n) | nlog n | クイックソート |
| O(n2) | 二次 | 2重ループを伴う配列全体の走査。バブルソートなど |
| O(n3) | 三次 | 3重ループを伴う配列全体の走査。行列計算など |
| O(2n) | 指数 | 集合分割問題 |
この表において、単純に言えば、上の方が計算量の小さい、つまり効率的なアルゴリズムであることを表しています。 しかし、現実的には必ずしもそうとはいえないことに注意が必要です。
また、データの個数を表す n は、それなりの大きさがあることを前提としています。 小さなデータ列を対象とすると、O(n) よりも O(n log n) の方が高速である可能性もあります。 しかし、データ列が大きくなっていけば、歴然とした差が出てきます。 n = 10 程度なら、O(n2) のアルゴリズムを使っても何ら問題ないでしょうが、 n = 100000 になったら、相当に酷い結果を生むでしょう。(図1-2.参照)
図1-2.オーダーと計算量計算量のグラフ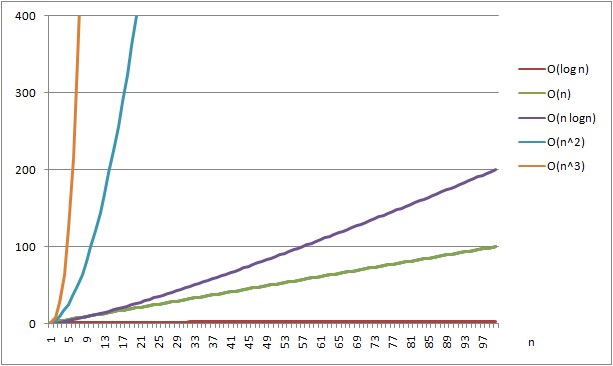
実際の処理時間との関係性
計算量によって、アルゴリズムの性能評価ができることから、これをもとにしてアルゴリズムの性能比較ができます。とはいえ、実際にプログラマーが最も興味があるのは、結局のところコンピュータ上でどれだけの処理時間が掛かるのかです。 理論上、あるアルゴリズムが効率的であると分かっていても、実測した結果、それでも遅いとなれば何とか対策を講じなければなりません。
現実的な路線で考える場合、計算量だけでは、1回分の実際の処理時間が考慮されていないことが問題になります。 ここでの「1回」というのは、先ほどの線形探索のプログラムで言えば、for文を1回繰り返すことに相当します。
ですから、他のアルゴリズムに取り替えたとき、そのアルゴリズムの for文の中身が線形探索のときよりもずっと複雑になるとすれば、 計算量としては O(n) から O(log n) に改善されたとしても、現実の処理時間は増加する可能性があるのです。








