バックトラック法
バックトラック法とは
コンピュータのアルゴリズムとは、みな多かれ少なかれ、何らかの問題の解決の糸口を求めるためのものです。アルゴリズムの中には、あらかじめある程度方法が確立されているものもあれば、そうでないものもあります。いや、そうでないものの方が、多いといっても良いかもしれません。
そのため、場合によっては、想定されるパターンを可能な限り洗い出してみて、その中から答えを導き出すしかないようなケースも存在します。とはいえ、そのパターンの数が膨大すぎては答えを導き出すことはできません。そのようなときに役に立つのが、バックトラック法(backtracking)といわれるものです。
この手法は、「すべてのパターンを系統的に探索して回答を得る」という手法で、探索の際に候補の数をできるだけ少なくおさえて、効率よく探索するのが最大の特徴です。
アルゴリズムのイメージ
抽象的な説明ではわかりづらいので、実際にバックトラック法は、どのようなアルゴリズムかということを、イメージを使って具体的に説明してきましょう。
バックトラック法の例として一番わかりやすい例は、迷路で、入り口から出口に至る道のりを見つけることです。スタートからゴールまでの道のりはいたるところで枝分かれしており、そこでの経路の選択次第では行き止まりになるか、ゴールにたどり着くか、ということになります。
入り口と出口が必ずつながっている迷路なら、各分岐点で選択肢を順番に、ひとつ残らず系統的に試していけば、この中から必ずゴールに到達できる道順がみつかるはずです。(図5-1.参照)このような考え方が、バックトラック法の基本的な考え方になります。
図5-1.トラックバック法と迷路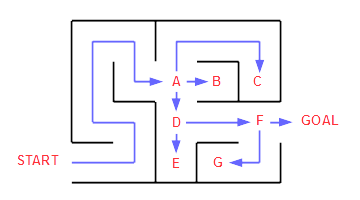
グラフとしての表現
このような問題は、グラフとして表現できます。スタート地点にいる状態をルートとして、分岐点に至ったとき、どちらに進むかによって、その状態をノードとして分岐させていき、探索していけば、出来上がったツリー構造の中から、ゴールに至る道のりに至る選択肢の組み合わせが一つ以上見つかるはずです。
図5-2.トラックバック法をツリーとして表記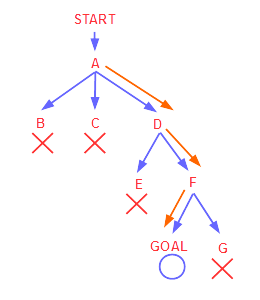
このように、選択した先に答えがあることがわかっているような問題を解決するには、バックトラック法という手法は有効なはずです。ただ、ゴールまでの道のりを見つける際に、問題によっては、
- ゴールへの経路が、どれでよいから1つだけ見つかればよい
- 全ての経路を発見しなくてはならない
- 全ての経路のうち、最も適切なもの(たとえば最短経路など)を見つけなくてはならない
といったように、問題ごとに求める答えが違ってきます。答えの候補となるものを見つけるまでは一緒ですが、それから先は、問題次第、ということになるわけです。
8クイーン問題
8クイーン問題とは
ここからは、バックトラック法を具体的な問題に当てはめてみます。バックトラック法の適用例として、もっとも有名な問題が、8クイーン問題(eight queens)です。
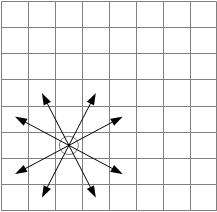
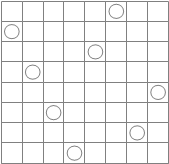
8クイーン問題とは、「8×8のチェス盤の上に、8つのクイーンを、互いに利き筋にあたらないように配置する」という問題です。チェスにおけるクイーンとは、将棋でいえば、核と飛車を併せ持ったような駒で、上下左右、および、斜め方向の8方向に自在に移動できます。(図5-3.参照)利き筋とは、駒が移動できる範囲を指しており、このことから利き筋と当たらない配置とは、ある場所に置いたクイーンの移動可能な経路の範囲内に、別の駒を配置しない、ということです。
図5-3.クイーンの移動方向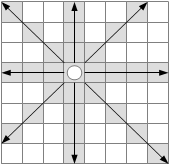
このことから、8クイーン問題の解答の一つは、以下のようになります。8つの駒すべてが、それぞれの利き筋にないことがわかるでしょう。(図5-4.) 図5-4.8クイーン問題の解答例
この問題を、チェス盤のサイズを一般化し、「n×nのチェス盤の上に、8つのクイーンを、互いに利き筋にあたらないように配置する」という問題に置き換えたのが、nクイーン問題と言われるものです。この問題は、数学で解析的に説く方法がない問題として知られており、回を求めるには、実際に盤面に駒を配置する必要があります。
問題の解法
では、実際にこの問題を解く方法を考えましょう。
(1) 総当たりでの問題解決
まず、この問題をクイーンの配置方法を総当たりで考えることによるコストを考えてみましょう。チェス盤には、8×8=64の場所があります。この任意の位置に、クイーンを1個配置すると、残りは63個になります。このように考え、8つのクイーンの配置方法を考えていくと、64×63×62×61×60×59×58×57 = 178,462,987,637,760パターンあり、総当たりで考えていくには無理があることがすぐにわかります。
(2) クイーンの性質を考慮に入れる
では、どうすれば現実的なパターン検索でこの問題を解くことができるでしょう?この時、ポイントになるのが、クイーンの駒の性質です。そもそも、クイーンは8方向に移動可能なので、一つのクイーンを配置すると、同じ列、同じ行に別のクイーンを配置することはできません。
そういったことから、クイーンは、各行に、1つしか配置できないことがわかります。そのため、このような場合は、8^8=16,777,216通りに減りました。ただ、これでもまだ数はまだまだ十分減ったとは言えません。
そこで、さらにもう一つの性質、各列に1つしか配置できないという性質をプラスします。すると、最初の列のクイーンの配置位置が決まると、同じ列に置けませんから、次の行で、クイーンを置ける行は7つになります。同様に、残りの行に関しても、組み合わせが6、5、4、…と減っていくことから、この組み合わせは8! = 8×7×6×5×4×3×2×1=40,320パターンにまで減ります。これぐらいの数なら、現実的な処理時間内で解決できそうです。
バックトラック法の適用
組み合わせを探索する数を十分に減らすことができたら、あとは探索にバックトラック法を適用するだけです。アルゴリズムの概略は、以下の通りになります。
- 0行目にクイーンを配置する位置を決める(図5-5.)
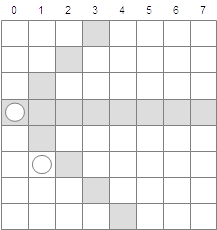
- 1行目に、0行目の利き筋ではない位置に、次のクイーンを配置する。(図5-6.)
- 2行目に、1行目の利き筋ではない位置に、次のクイーンを配置する。(図5-7.)
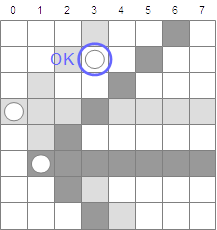
- 2行目に配置したクイーンが、0行目のクイーンの利き筋に配置されていたら、3.に戻り、1行目の配置をやり直す。(図5-8.)
- 3行目に、2行目の利き筋ではない位置に、次のクイーンを配置する。
- 3行目に配置したクイーンが、0行目、1行目のクイーンの利き筋に配置されていたら、5.に戻り、3行目の配置をやり直す。 …
| 図5-5.0行目の配置 | 図5-6.1行目の配置 |
|---|---|
 |
 |
| 図5-7.2行目の配置(成功) | 図5-8.2行目の配置(失敗) |
 |
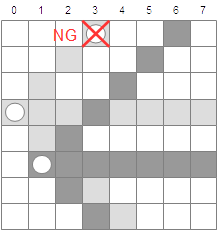 |
要約すると、次々と、直前の行の利き筋ではない位置にクイーンを配置していき、配置したものが、その前に配置してきたすべてのクイーンの利き筋でれば、その配置をあきらめ、そうでなければ次にいき、最後まで配置できたものが、その答えになる、というアルゴリズムです。
その他のアルゴリズム
ナイト巡回問題
8クイーン問題は、バックトラック法の最も代表的なアルゴリズムの例と言えるでしょう。このほかにも、このアルゴリズムが適用できる有名な事例として、8クイーン同様、チェスを題材とした問題である、ナイト巡回問題と呼ばれるものがあります。
ナイト巡回問題とは, 「1つのナイトをチェス盤上に置き,同じ場所を通ることなく動かし、チェス盤の全てのマスを通過させて始めの場所に戻せ」 というものです。ナイトは、将棋の桂馬のような動きをする駒ですが、桂馬との大きな違いは、前後左右、合計8つの方向に動くことができるという点にあります。(図5-9.)
図5-9.ナイト巡回問題