一週間で身につくアルゴリズムとデータ構造|入門編6日目：アルゴリズムの例③

整数に関する基本的なアルゴリズム

最大公約数と素数

続いて、二つの数値の最大公約数を求める、ユークリッドの互除法（ごじょほう）というアルゴリズムと、素数を求めるアルゴリズムである、エラトステネスのふるいを紹介します。

まず、最大公約数について説明します。数値mがnで割り切る時します。このとき、nはmの約数であると言います。具体的に言うと、4は2で割り切れるので、2は4の約数であると言えます。また、2つの数m1,m2があった時、nがその両方の約数であれば、nはm1とm2の公約数と言います。例をあげると、12と18の約数として、2と3があります。このような、公約数のうち、最大のものが最大公約数です。

続いて、素数について説明しましょう。素数とは、1と、その数自身（1は除く）しか、約数を持たない自然数のことを言います。例えば、5の約数は、1と5だけなので、素数であるといます。しかし、6は、2と3という約数を持つので、素数ではありません。ユークリッドの互除法とは、ある数までの範囲内にある、素数をすべて探し出すためのアルゴリズムです。以下、それらアルゴリズムを順を追って説明していきます。

ユークリッドの互除法

アルゴリズムの実装

ではまず、ユークリッドの互除法から説明していきましょう。アルゴリズムは前述のように非常にシンプルなものです。それを、より丁寧に記述すると、以下のようになります。ここでは、最大公約数を求めたい2つの整数を、m、nで、m>nであると仮定します。また、更に作業用の変数dを用意するものとします。

手順1.	変数dにmとnの割り算の余りを代入する。
手順2.	dが0なら、nを最大公約数として出力する。
手順3.	mにnの値を代入する。
手順4.	nにdの値を代入する。
手順5.	手順1に戻る。

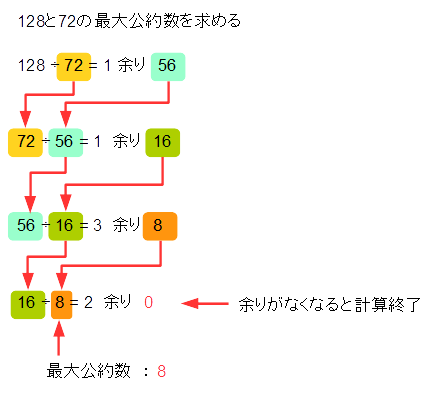
これを、具体的な数値の例を出すと、以下のようになります。（図6-1.)この図から見ればわかるとおり、128と72の最大公約数は、16であることがわかります。

図6-1.ユークリッドの互除法

C言語による実装

エラトステネスのふるい

エラトステネスのふるいとは

エラトステネスのふるいとは、ある自然数nまでの素数をすべて求めるための方法です。考え方は非常に単純で、1からnまでの数値の票を用意して、明らかに素数である2を残し、その倍数である、4,6,8,…を消していきます。それが終わると、2の次にある、消えていない数3が次の素数となるので、2の場合と同様に、その倍数である、6,9,12…などを消していきます。この要領で、次の素数5,7…で同様の処理を繰り返していくと、最終的に残った数値は、すべて素数になります（図6-2.）。これが、エラトステネスのふるいという考え方です。

図6-2.エラトステネスのふるい

用意するデータ構造

このアルゴリズムを実現するために、必要なデータ構造として、2つの配列を定義することにします。

一つ目として、要素数n+1の配列dataを用意します。これにより、N+1個の配列変数である、data[0],data[1],…,data[n]が得られます。

この配列には、初期状態として、すべて値1を代入しておくことにします。最終的に、処理が終わると、この番号に相当する数の要素の値が1であれば、その数は素数、そうでなければ、素数でないという判定を行うためにこの配列を用います。

二つ目として、素数の出力結果を格納する配列、resultを用意します。resultの大きさは、dataと同じく、N+1であるとします。なぜこの要素数となるかというと、出力される素数の数は不明ですが、dataの要素数を超えることがかに為、同じサイズの要素数であれば、確実に格納できるからです。一見無駄に見えますが、配列を使用し、その出力結果の数がわからないので、このようなサイズの配列を用意しておくことにします。この配列には、dataで得られた素数を入れておくものとします。

アルゴリズムの手順

では、具体的なアルゴリズムの手順を見てみることにしましょう。

手順1.	変数mを用意し、2を代入する。（この変数は、配列dataにアクセスするためのもの)
手順2.	変数nを用意し、0を代入する。（この変数は、配列resultにアクセスするためのもの）
手順3.	配列dataの値を全てすべて1で初期化する。
手順4.	配列resultの値を全てすべて0で初期化する。
手順5.	data[0]、data[1]に、0を代入する。（あらじめ素数でない数は排除する）
手順6.	変数iを用意し、iに2×mを代入する。
手順7.	iがN未満の間、data[i]に、0を代入し、iにmを足すという処理を繰り返す。
手順8.	result[n]にmを代入する。
手順9.	nをインクリメントする。
手順10.	mをインクリメントする。
手順11.	mがNより大きくなったら、手順13へ。
手順12.	data[m]が1ならば、手順6へ。
手順13.	resultの値を出力し、処理を終了する。