素因数分解
素因数分解とは
最後に、整数型配列を用いた基本的なアルゴリズムの集大成として、素因数分解(そいんすうぶんかい)を紹介します。アルゴリズムについて説明する前に、そもそも素因数分解とは何かということについて説明します。
任意の自然数は、かならず複数の素数の掛け算として、表現できます。たとえば、12という数は2×2×3、42という数は、2×3×7、といった具合に、素数の積で表現されます。このように、自然数を素数の積にまで分解することを、素因数分解と言います。ここでは、それを行うアルゴリズムを考えてみることにします。
シンプルなアルゴリズム
すでに、いくつかのアルゴリズムを見てきたので、素因数分解のアルゴリズムは、複数のアルゴリズムが組み合わさったものだということがわかると思います。アルゴリズムの一つ目は、エラトステネスのふるいです。これで、素因数分解したい数以下の素数をすべて求めれば、その数のなかから、その数の約数となるものと、その数・組み合わせを求めればよいのです。
したがって、処理の手順は以下の通りになります。なお、この処理を行うに際し、素因数分解を行いたい数が入った変数nと、素因数の値を入れる配列pfを用意します。pfの要素数は、nにします。
| 手順1. | エラトステネスのふるいを用い、nまでの素因数分解を行い、得られた結果を、配列変数resultに代入する。 |
| 手順2. | 変数iを用意し、0を代入する。 |
| 手順3. | 変数jを用意し、0を代入する。 |
| 手順4. | result[i]で、nを割った余りが0であれば、その値をpf[j]に代入し、jに1を足し、手順6に飛ぶ。 |
| 手順5. | result[i]で、nが割り切れなければ、iに1を足す。 |
| 手順6. | nに、nをresult[i]で割った値を代入する。 |
| 手順7. | nが1でなければ手順4に戻る。 |
| 手順8. | pf[0]からpf[j]までの値を、素因数として出力する。 |
これを、図に表わすと、以下のようになるす。(図7-1.)つまり、エラトステネスのふるいの結果がある配列、resultから、素数を一つづつ取得し、その値で目的の数値を割り切れれば、それを格納し、最終的に値が1になるまで、繰り返すというものです。
図7-1.素因数分解のアルゴリズム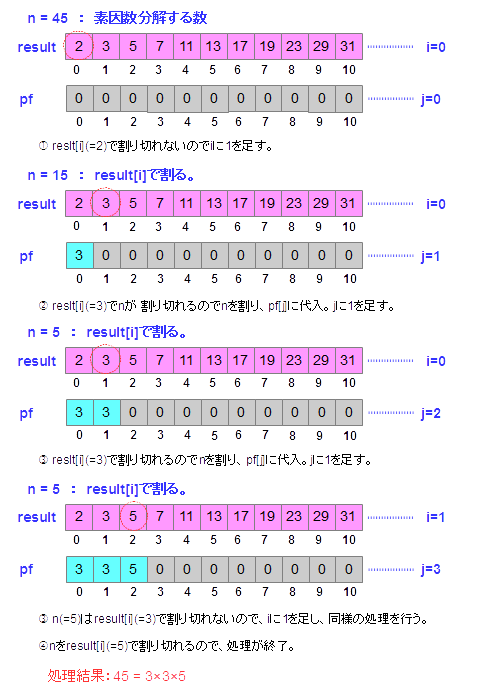
アルゴリズムの問題点
このアルゴリズム自体は正しく動作するため、正しい結果を得るための手順としては、間違いではありません。しかし、アルゴリズムが正しいからと言って、それが適切な方法とは限らないのです。
なぜなら、アルゴリズムをプログラムとして実現するコンピュータには、処理速度や記憶容量などの様々な制限があるため、アルゴリズムはなるべく早い処理速度で、かつメモリも無駄に使うことなく実現されるのが理想とされるのです。
そういった観点から、このアルゴリズムを眺めると、必ずしも適切とは言えません。例えば、128という数値を素因数分解すると、「2×2×2×2×2×2×2」となると、必要な素数は2の一種類しかないことがわかります。
ところが、128までの素数は、39個もあり、それらすべての素数を求めるということは、それだけ処理の時間と、メモリを浪費してしまうことになります。これは大変無駄なことです。
アルゴリズムの改良
では、どうすればこのアルゴリズムの無駄を抑えることができるでしょうか?方法はいろいろあるとは思われますが、実は意外とシンプルな方法が存在します。
それは、素因数分解したい数をnとするとき、nの最大の約数となるmを見つけると、nと、mの約数は、素数になります。続いて、nに、mを代入して、同様の方法を行うというものです。具体的な手順は、以下のようになります。
| 手順1. | mに、nを代入する。 |
| 手順2. | 変数iを用意し、iに0を代入。また、結果を入れる配列pfを用意し、0で初期化する。 |
| 手順3. | mから、1を引く。 |
| 手順4. | nが、mで割り切れなければ、手順3.に行く。 |
| 手順5. | 変数dを用意し、n/mを代入する。 |
| 手順6. | pf[i]に、dの値を代入し、iに1を足す。 |
| 手順7. | nをdで割る。 |
| 手順8. | nをdで割ったあまりが0ならば、手順6.へ行く。 |
| 手順9. | mにnを代入する。 |
| 手順10. | nが1でなければ、手順3に戻る。 |
| 手順11. | pf[0]からpf[i]までの値を、素因数として出力する。 |
説明だけでは分かりづらいので、この処理の流れを、図で表現してみましょう。図にあらわすと以下のようになります。(図7-2.)
図7-2.改良後の素因数分解のアルゴリズム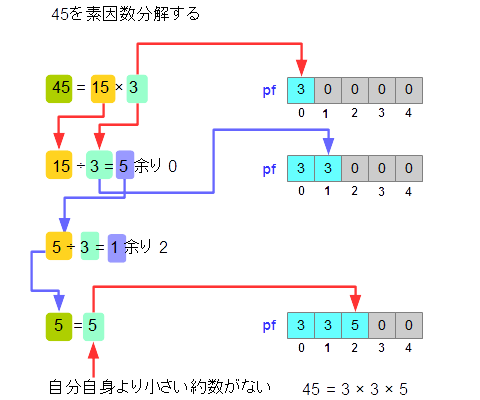
結果を見てもわかるとおり、このアルゴリズムを用いれば、エラトステネスのふるいで、すべての素数を求めるのではなく、エラトステネスのふるいを実行し、素数が出るたびに、その数で素因数分解ができるかを検証するので、無駄な計算を省くことができます。
アルゴリズムの改良
様々なアルゴリズム
この素因数分解の例からもわかるとおり、一つの問題を解くためには、さまざまなアルゴリズムが存在します。また、どんな複雑なアルゴリズムも、いくつかの基本的なアルゴリズムの組み合わせに過ぎません。
つまり、プログラマーは、一つの問題を解くために、さまざまなアルゴリズムの中から、適切なものを選び、適切な形で組み合わせることが求められるのです。
データ構造の重要性
また、この入門編であつかったデータ構造は、変数、もしくはその配列のみで、非常に原始的なものでした。しかし、これだけでは様々なアルゴリズムを記述するには不十分なのです。つまり、アルゴリズムの質を向上させるためには、セットでデータ構造について学んでいく必要があるのです。
基本編では、それらの諸事情を勘案し、さまざまなデータ構造と紹介し、それらを用いたアルゴリズムについて紹介していきます。








