2進数と16進数
2進数を使う理由
既に基本編で説明したとおり、コンピュータの内部では、 数値は 2 進数 (binary number) で表されています。10 進数 (decimal number) とは違い、2進数には、数字が0と1しかなく、 大変わかりづらいものです。
たとえば、 433,919 という数字を2進数で表すと、 1101001111011111111になります。このように、0 と 1 ばかりだと、人間には大変わかりづいらいものです。しかし、この2進数を用いるからこそできる様々な処理があります。
そこで、ここでは2進数と、それと深い関係にある16進数についてより詳しく説明し、その理論と利用方法について学んでいきます。
2進数と10進数
10進数と基数
2進数について説明する前に、そもそも10進数とはどういう数なのか、考えてみましょう。10進数では、0から9 の10種類の数字を使って数値を表します。たとえば、10進数で 238 と書けば、10進数の各桁にそれぞれ102、101、100(=1) の重みがある、ということになります。つまり、
ということになるのです。10進数の場合、 1桁左に書かれた数字は、 1桁右の数字よりも10倍の重みを持っています。 この数字 を、 基数 (radix) といいます。 10進数の基数は 10 です。
2進数から10進数への変換
それに対し、2進数は、2を基数とする数のことです。2進数の各桁にも10進数同様それぞれ重みがあり、 1桁左に書かれた数字は、 1桁右の数字よりも 2倍の重みを持っています。 たとえば、2進数で1101 と書けば、
となります。このように、2進数は10進数に変換することにより、人間にとって理解・取り扱いが容易な表現に変更することが可能です。
10進数から2進数への変換
今度は、10進数を2進数に置き換える方法について説明していきましょう。簡単な例として、13という数値を2進数に置き換えてみます。基本編で学んだとおり、10進数を2進数に置き換える場合、その数を2で割り、余りがあれば最初の数を1、なければ0とし、その答えをさらに2で割り、同じく余りがあれば1、なければ0、をならbて行くことによって、結果を得ることができます。したがって、13を2進数に変換すると、1101となります。
図1-1.10進数から2進数への変換①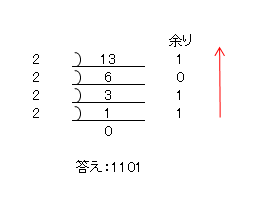
では一体、なぜこのようにして2進数の値を得ることができるのでしょうか?これは、13という数を2の基数とした場合の表現の仕方を見れば、わかります。13はもともと、
と表せます。これを2で割ると、答えは6、余りは2となります。更に、
となりますさらに2で割ると、答えは3、余りは0となります。 (2で割った余りが0)
となり、最後の答えが1となり、余りと最後の数を並べると、1101となります。以上からわかるとおり、2で割ることにより、二進数の桁が一つづつ右にシフトしていくため、そこからはみ出た数を並べていくだけで、自然に2進数が得られるわけです。つまり、2で割り続け、その結果得られた余りを並べることにより、2進数を得られるということがわかります。(図1-2.)
図1-2.10進数から2進数への変換②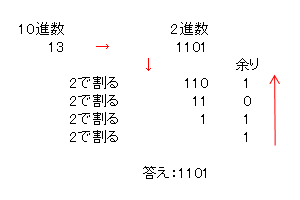
16進数
16進数の表現
2進数や16進数の場合と同様、16進数は 16 を基数 として表した数値です。10進数は 0 から 9 までの 10種類の数字を使って数を表し、 数が 0 から 1、2、3… と順に増えていくとき、7、8、9 までは 1桁ですが、 次は桁上がりして 10 になります。
それに対し、16進数には 16種類の数字がありますが、 文字としての数字は 0 から 9 までの 10種類しかないので、 アルファベットの A ~ F (小文字を使うこともある)を数字として利用します。そのため、16進数で「10」と表される数は、10進数の16ということになります。10進数と16進数の対応は、以下のようになります。(表1-1.)
表1-1:16進数と2進数の対応| 10進数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 16進数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
16進数から10進数への変換
では、続いて16進数を10進数に変換する方法を見てみましょう。16進数の場合も、2進数同様、それぞれの桁の重み付けをおこない、各けたの重みをかけたものの合計を求めれば10進数を得られます。たとえば、1FAという値は、
となります。
10進数から16進数への変換
逆に、10進数から16進数に変換する方法をみてみましょう。16進数の場合も、2進数の場合と同様、10進数の値を基数である16で割り、そのあまりを逆から並べれば完成です。ただし、この際気をつけなくてはならないのは、余りとして得られる値を16進数に置き換えることです。(図1-3.)
図1-3.10進数から16進数への変換②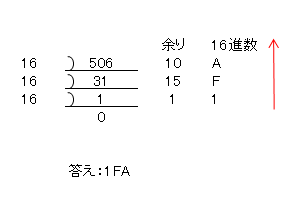
16進数と2進数の関係
1バイトと16進数
一見無関係に見える2進数と16進数ですが、実は密接に関連があります。実は16進数とは、2進数をよりわかりやすく表現するために便利な表記方法なのです。
コンピュータの最小単位は、「0」か「1」かのビット(bit)の単位で表しますが、ある程度まとまったデータの場合の最小単位は、1バイト=8ビットで表されます。この8ビットを半分の4ビットに分割すると、「0000」から、「1111」までの16のパターンを表現できます。つまり、これは、16進数の数値が表現できるデータなのです。(表1-2.)
表1-2:16進数と2進数の対応| 10進数 | 16進数 | 2進数 | 10進数 | 16進数 | 2進数 |
|---|---|---|---|---|---|
| 0 | 0 | 0000 | 8 | 8 | 1000 |
| 1 | 1 | 0001 | 9 | 9 | 1001 |
| 2 | 2 | 0010 | 10 | A | 1010 |
| 3 | 3 | 0011 | 11 | B | 1011 |
| 4 | 4 | 0100 | 12 | C | 1100 |
| 5 | 5 | 0101 | 13 | D | 1101 |
| 6 | 6 | 0110 | 14 | E | 1110 |
| 7 | 7 | 0111 | 13 | F | 1111 |
このことからわかるとおり、16進数は8ビットの数を4ビットごとに分かりやすい表記方法に変えてくれる表記方法であることがわかります。8ビットであらわされる数値は、0~255の256パターンですが、これは16進数で表すと、「00」から「FF」にあたります。また、倍の1ワード=16ビットであれば、0~65,535の65,536パターンですが、これも16進数で表すと、「0000」から「FFFF」にあたります。
つまり、8ビット、および16ビットでの数値は、10進数よりもはるかに見やすい数値になっていることがよくわかります。









