2進数の加算と減算
2進数の計算
続いて、2進数の計算について説明します。2進数の演算には様々なものがありますが、手始めに加減乗除などの、算術演算(さんじゅつえんざん)について説明します。手始めに紹介するのは、加算と減算です。
基本的に、2進数で計算しても、計算結果は10進数と結果に変わりはありません。ただ、2進数で計算する場合には独特の特徴があります。ここでは、計算の仕方と同時に、そういった特徴について説明します。
2進数の加算
2 進数 には数字は0と1だけしかありません。そのため2進数の加算も次の表の4種類しかありません。(表2-1.)1と1を足したときだけ、桁上がりがおこり、2進数の10(10進数の2)となるのです。
表2-1:2進数の数の加算の組み合わせ| A | B | A+B | |
|---|---|---|---|
| 2進数 | 10進数 | ||
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 10 | 2 |
では、これをもとに実際の計算をしてみましょう。2進数0101(10進数の5)と0010(10進数の2)を足してみましょう。図2-1.のとおり繰上げは生じませんので解は0111です。0111は10進数の7ですから、2進数で表現しても10進数で表現しても同じ値を意味することがわかります。(図2-1.)
図2-1.2進数の足し算(繰り上げなし)
今度は繰り上げが生じるパターンをみてみましょう。0101と0111を足してみます。すると、図2-2.のようになります。下から3桁目で1が繰り上がってきて、それに1を足しさらに1を足します。1+1+1=3ですから2のグループがひとつできて1余ります。2のグループが1つですのでやはり1繰り上がります。余った1をそのまま下に記述します。(図2-2.)
図2-2.2進数の足し算(繰り上げあり)
2進数から10進数への変換
それに対し、2進数は、2を基数とする数のことです。2進数の各桁にも10進数同様それぞれ重みがあり、 1桁左に書かれた数字は、 1桁右の数字よりも 2倍の重みを持っています。 たとえば、2進数で1101 と書けば、
となります。このように、2進数は10進数に変換することにより、人間にとって理解・取り扱いが容易な表現に変更することが可能です。
2進数の減算
続いて、ひきざんのケースを見てみましょう。まずは、単純なケースとして、1110-0110を計算してみます。これは繰り下がりが発生しないため、素直に引き算を行えばよいので、非常に単純です。(図2-3.)
図2-3.2進数の引き算(繰り下げなし)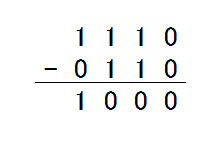
続いて、繰り下がり(上位桁から借りてくる)が発生する場合のケースを考えてみます。上位桁の1はそのすぐ下の桁で2のグループができたので繰り上がったわけですから、借りてきたら下位桁では「2」であるとと考えます。
では、この考え方をどのようにして利用すればよいのでしょうか。実際に、1101-0110を計算してみましょう。最下位桁は1-0なので1をそのまま記述します。下位第2桁は、0から1は引けないので上位桁から借りてきます。1を借りてくるのですが、自分の桁に直すと2ということになりますから、2-1で1を記述します。下位第3桁は1貨していますので0です。0から1は引けないのでまた上位桁から借りてきて、2-1の計算をします。(図2-4.)
図2-4.2進数の引き算(繰り下げあり1)
続いて、繰り下がりありのケースをもう一例見てみましょう。(図2-5.)1001-0110のケースを考えてみます。この差は十進数で考えれば、9-6で、3になります。最下位桁は、1-0なので1をそのまま記述します。しかし、下位第2桁は、0から1は引けないので上位桁から借りてきて、自分の桁で2とし、2-1で1を記述します。(①)
ところが、下位第3桁は0なので、もともとそこから1を借りることができません。そこで、最上位桁から借りてきて、下位第3桁を2とし、さらに、下位第3桁に1貸したため、そこから1をひいて、1とします。(②)そのため、下位第2桁は、1-1の計算をし、0が得られます。その結果、最上位の桁は0となり、0-0で0が得られます。
図2-4.2進数の引き算(繰り下げあり2)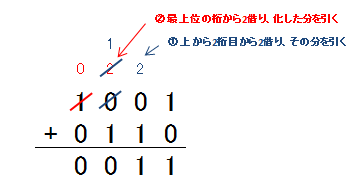
負の数の表現
2進数で負の数を表す
10進数同様、2進数でも負の数を表すことができます。しかし、コンピュータの中で、有限桁の2進数で負の数を表す方法は少し特殊な考え方を必要とします。ここでは、そういった場合に限定して、2進数で負の数を表す方法について学習します。ここではまず、もっともよくつかわれる、8ビット=1バイトの場合の表現について考えてみることにします。
1バイトでは、8桁(8ビット)なら2×2×2×2×2×2×2×2(2の8乗)で256種類の数値を表すことが可能です。そのため、通常8ビットで整数を表す場合は、00000000を0、11111111を255として、0~255の256種類の数値を表すことが可能です。
しかし、8ビットの数を用いて負の数を表す場合はどうすればよいのでしょうか?その場合、00000000が「0」であることは変わりません。また、00000001を「1」、00000010を「2」…といった増え方をしていくのも変わりません。
では、負の数をどのように表現するのかというと、「-1」はどのようにして表現するかというと、「11111111」を「-1」、「11111110」を「-2」…といった風に考えることにします。すると、8ビットの2進数で表現できる正の数は1(=00000001)から127(=01111111)までとなり、負の数は、-1(=11111111)から、-128(=10000000)までとなります。(図2-6.)
図2-6.8ビットによる正の数と負の数の表現
図から見てわかるとおり、正の数は必ず先頭のビットが「0」となり、負の数の場合は「1」となっています。2進数で正負の数の区別するものは、この先頭のビットの値です。
10進数の負の数を2進数に変換する場合
以上が8ビットの場合の2進数の正の数・負の数を考える場合のやり方です。では、具体的に「-10」や「-98」などといった数値を2進数にした場合は、どのようになるのでしょうか?今度は10進数の負の数を2進数に変換する場合を考えてみましょう。
このケースも前のケース同様、8ビットの場合で考えてみるとします。その際に大事になってくるのが、2進数の正負を逆転する方法です。すでに説明したとおり、+1は、「00000001」、-1は、「11111111」となり、+2は「00000010」、-2は「11111110」です。更に大きな数でこの関係を見ていると、正負の数の変換には、以下のようなルールがあることが分かります。(図2-7.)
① 2進数の0と1をすべて入れ替える② ①の値に1を足す。
具体的な例をあげると、+1の「00000001」の0と1を逆転すると、「11111110」となり、これに1を足すと、「11111111」となり、-1になります。逆に、「11111111」のビットを反転させると、「00000000」となり、1を足すと「00000001」つまり、+1であることがわかります。(図2-9.)
図2-7.2進数での正負の数の逆転
妥当性の検証
このようにしてビット数が限られている2進数の場合は、2の補数を得ることにより政府の逆転ができるということがわかりました。ただ、問題ははたしてこの表現方法がだというかということです。そこで、この方式で、正の数と負の数を足すことにより、結果がその引き算になるかどうかを検討してみましょう。
試しに、6-3の計算を、+6( = 00000110)と、-3( = 11111101)の足し算によって行う計算をしてみましょう。この二つを足すと、結果は2進数で「100000011」となります。ここではビット数を8ビットに限定しているので、桁あふれした最上位の1をカットすると、結果は「00000011」となります。これは10進数に直すと3ですから、計算の結果は妥当であることが分かります。(図2-8.)
図2-8.正負の数の足し算による引き算
つまり、この考え方は単にある数値を負の数に置き換えただけではなく、きちんと演算処理も行えるということがこれからわかります。
概念の一般化
補数
さらなる説明をする前に、ここで、補数(ほすう)という大事な概念について説明します。補数というのは、文字どおり「補う数」です。たとえば37という数値があったとします。2桁で表される最高の数は99です。あと62で99になります。この62が37に対する「9の補数」といいます。また、あと63で桁上がりして100となります。桁上がりする最低の数63が37に対して「10の補数」と言います。
図2-9.10の補数と9の補数
少し難しい表現になりますが、一般的に言うと、ある自然数をn進数で表現した時に、足し合わせるとちょうど「nのべき乗」か「nのべき乗-1」になる自然数のうち、最小のものを、補数と言います。前者は足すとちょうど桁が一つ増える数で、基数の補数とも呼ばれ、後者は足しても桁が増えない最大の数で、減基数の補数とも呼ばれます。
2の補数と1の補数
つまり、10進数では、67にとって、33は、足すとちょうど100、つまり102となるので、基数の補数、32は足すとちょうど99、つまり102-1となるので、減基数の補数となるわけです。
このように、各進数には桁上がりする補数とそれより1小さい補数が必ず定義されています。2進数ならば、2の補数と1の補数が定義されることになります。2の補数は、足し合わせるとちょうど2のべき乗であり、1の補数は桁上りせずちょうど2のべき乗-1(2進表記で1111…)となるものです。
これをよりわかりやすく言いかえると、1の補数はビットを反転したもの、さらに、2の補数は1の補数に1を足したものということになります。(図2-10.)
図2-10.2の補数と1の補数
再び2進数での正負の逆転
以上からわかるとおり、2進数のある数の正負を逆転するということは、その数の2の補数を得る、つまり、1の補数に1を足す、という処理であることがわかります。このようなことから、2進数で扱う桁数が違っても同じ方法で正の数・負の数の変換ができるということがわかりますし、実際にコンピュータの内部ではそのようにして演算処理を行っています。
以下の表(表2-1.)は、C言語で用いられている主要な基本データ型とそのサイズおよび扱える数値です。ビット数は違っても、コンピュータの中ではまったく同じ方法で正負の表現をしています。また、符号を持たないデータ型は、素直にその値を正の10進数の値に変換していることから、扱える値の範囲は倍になります。
表2-1.C言語の主要な基本データ型| データ型 | 説明 | 範囲 |
|---|---|---|
| char | 1バイトの符号付整数。ASCIIコードといった文字コードに使用。 | -128~+127 |
| unsigned char | 1バイトの符号なし整数。 | 0~255 |
| short | 2バイトの符号付整数。 | -32768~32767 |
| unsigned short | 2バイトの符号なし整数。 | 0~65535 |
| long | 4バイトの符号付整数。 | -2147483648~2147483647 |
| unsigned long | 4バイトの符号なし整数。 | 0~4294967295 |
| int | 2または4バイトの符号付整数。(コンパイラに依存) | |
| unsigned | 2バイトまた4バイトの符号なし整数。(コンパイラに依存) |
言語としては、C言語の場合について説明しましたが、基本的には他の主要な言語でもかわりません。また、マシン語でCPUの中で数値を扱う場合も、まったく同じ考え方で処理されています。









