シフト演算
シフト演算とは
続いて、二進数のシフト演算について説明します。加算・減算は算術演算と呼ばれる演算の一つですが、ビット演算はそこには含まれない特殊な演算です。シフト演算とは、二進数のビットをずらす(シフトする)だけの非常に単純な演算です。実はさまざまな演算がこのシフト演算に関連しており、2進数の演算としては非常に大事な処理の一つです。
シフト演算には、大きく分けて、論理演算と算術演算があり、それぞれ必要に応じて使い分けます。ここでは、それぞれのケースのシフトの方法と、その使い分けについて説明します。
論理シフト
前述の通り、シフト演算とは、2進数のビットを右、または左にずらすだけの演算です。シフト演算には右シフトと左シフトがあり、右シフトは連続したビットを右に、左シフトはビットを左にずらします。(図3-1.)このとき、空いたビットには「0」が入れられていますが、このようにシフトによって空いたビット位置すべてに0を入れるようなシフトの処理のことを、論理シフトと言います。(図3-1.)
図3-1.論理シフト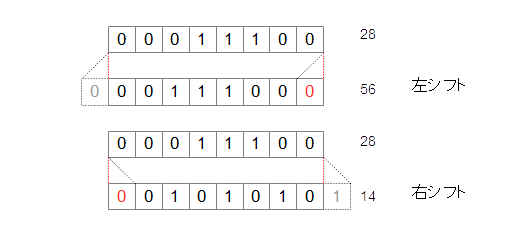
では、シフト演算には一体どのような意味があるのでしょうか?2進数の各桁は2のn乗なので、左に1回シフトするごとに値は常に2倍となり右に1回シフトするごとに値は半分になる(2で割る)ということになります。つまり、スフと演算を複数行えば、4倍、8倍といった計算や、1/4、1/8といった計算ができるわけです。
しかし、その時気をつけなけらばならないのが、2日目で説明した負の数をあつかうようなケースです。たとえば、8ビットの符号付きの整数えで11100100は、-28ですが、左に論理シフトを行うと01011010となり、10進数で表現すると-56ですがこれを右に論理シフトすると、01011010となり、10進数で表現すると90になってしまいます。つまり、符号付きの整数を論理しるとすると、符号が変わってしまうのです。
図3-2.論理シフトで符号が変わってしまうケース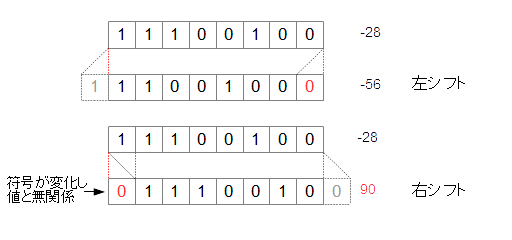
このように、論理シフトではシフトにより値が2倍、4倍、もしくは1/2、1/4になる、というルールが適応できなくなるのです。そこで、こういったケースで用いるのが、算術シフトと呼ばれるものなのです。
算術シフト
では、算術シフトとはどのような演算なのでしょうか。算術シフトは、基本的に符号を維持するために、以下のようなルールがあります。
(1)最上位の符号ビットは固定する(2)左シフトの場合は空白のビットを0で埋める (3)右シフトの場合は空白のビットに符号ビットを埋める
では、実際に正の数の場合と負の数の場合で見てみましょう。正の数の00011100(=+28)を左シフトすると、00111000(=+56)となり値が倍、右シフトすると00001110(=+14)となり、論理シフトと同じっかが得られることが分かります。(図3-3.)
図3-3.算術シフト(正の数の場合)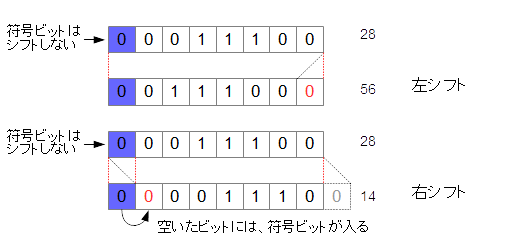
続いて、負の数のケースを見てみましょう。11100100(=-28)を左シフトすると、11001000(=-56)となり、符号が保たれたまま値が倍になっています。それに対し、右シフトは論理シフトの場合と違い、空各部に符号ビットの1が入りますから、結果は11110010(=-14)となり、符号を保ったっままで値が半分になっていることがわかります。(図3-4.)
図3-4.算術シフト(負の数の場合)
以上のことから、算術シフトを用いれば、符号を保ったままで値を倍増、半減させることができるということがわかります。
シフト演算の用途
こういったシフト演算の用途は、かつては、プログラミングの領域で2倍、4倍のような掛け算や、1/2、1/4といった割り算を行うために使われていました。しかし、現在はコンピュータの性能の向上やコンパイラの性能の向上で余り用いられなくなりました。
しかし、2のn乗での乗算や除算以外でも、掛け算、割り算でシフト演算を使う必要があるのです。そこで、次は実際に2進数の掛け算、割り算を見てみましょう。
二進数の乗算・除算
2進数の積
2進法で表わされた数の積は,各位の数について、以下の規則によって計算されます。(表4-1.)各位の積はこのように単純なものです。しかし、実際の計算では加えるときの桁上がりに注意する必要があります。
表4-1:2進法で表わされた数の積| A | B | A*B | |
|---|---|---|---|
| 2進数 | 10進数 | ||
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
まずは、非常に単純な計算の例を見てみましょう。2進数の10(=2)と2進数の10(=2)の乗算を行ってみます。やり方は10進数の掛算の場合と同様に行います。(図3-5.)
図3-5.乗算の例①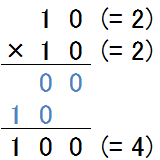
続いて、もう少し桁の多い場合の例を見てみましょう。111(=7)と、11(=3)の乗算を行うと、以下のようになります。(図3-6.)結果が10101(=21)となり、10進数と同じ結果であることが分かります。
図3-6.乗算の例②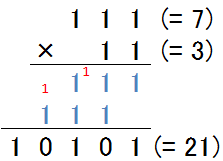
例からもわかる通り、2進数の乗算は最初の数をシフト演算でずらしながら足していくものであるということが分かります。
2進数の商
続いて、2進数の割り算を見てみましょう。除算の場合も、10進数の場合とまったく同じです。まずは、あまりが出ない場合のケースを見てみます。0110(=6)と011(=3)の割り算を見てみましょう。結果から見てわかる通り、答えが10(=2)となることがわかります。(図3-7.)
図3-7.除算の例①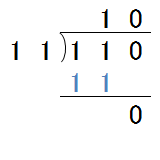
続いて、あまりが出るケースを見てみましょう。1110(=14)と100(=4)の割り算を見てみます。答えが10(=2)であり、あまりが11(=3)であることがわかります。(図3-8.)
図3-8.除算の例②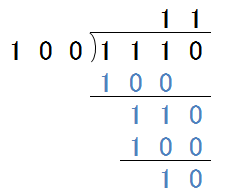
掛け算が左側への論理シフトした値の和によって求められるものであったのに対し、割り算は右シフトによる引き算の積み重ねであることが分かります。









