論理回路
コンピュータの基本の回路
なんども言及している通り、コンピュータは「0」および「1」という2つのパターンのみしか認識できません。そんなコンピュータの根幹をなす部品・回路のことを、論理回路(ろんりかいろ、英: logic circuit、ロジック・サーキット)と言います。
これは、論理演算を行う電気回路及び電子回路で、真理値の「真」と「偽」、もしくは2進法の「0」と「1」を、電圧の正負や高低などで表します。最後に今まで紹介してきた演算を実際に行う回路について説明します。
組み合わせ回路
論理ゲート
論理回路には様々な種類のものが存在しますが、ここでは演算と縁の深い組み合わせ回路について説明します。組み合わせ回路は、現在の入力のみで出力が決まる回路で、様々な種類がありますが、まずは基本である論理ゲートについ説明します。
論理ゲートとは、AND(アンド)、OR(オア)、NOT(ノット)、XOR(エクスクルーシブ・オア)など基本となる論理演算を行うものです。論理ゲートの表記の仕方は様々ですが、ここではその中の1つである、MIL記号で表現します。(表7-1.)
表7-1.論理ゲート| 論理 | 論理式 | 回路記号(MIL記号) |
|---|---|---|
| NOT | 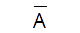 |
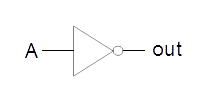 |
| OR | 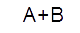 |
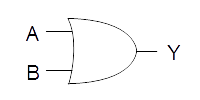 |
| AND | 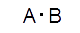 |
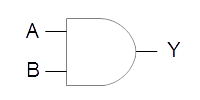 |
| XOR | 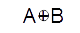 |
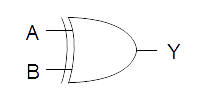 |
| NOR | 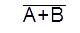 |
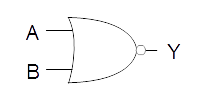 |
| NAND | 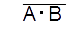 |
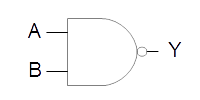 |
加算器
組み合わせ回路のうち、加算をおこなうもののことを、加算器(かさんき)と言います。加算器は、基本的な論理ゲートの組み合わせで構成されています。
加算器について説明する前に、まずは基本となる半加算器(はんかさんき:half adder)について説明します。半加算器とは、下位けたからのけた上がりを考えない中途半端な加算回路だからです。半加算回路をMIL記号で表すと以下のず(図7-1.)のようになります。2つの論理演算を組み合せていることに注目してください。
図7-1.半加算器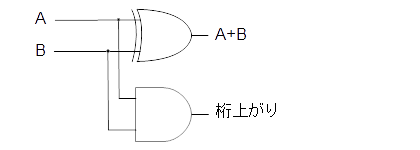
これに対し、桁上がりも考慮する加算器のことを、全加算器(ぜんかさんき:full adder)と言います。全加算回路は,入力が3つあります。該当するけたの2つの値と,下位けたからけた上がりした値で3つです。
図7-2.全加算器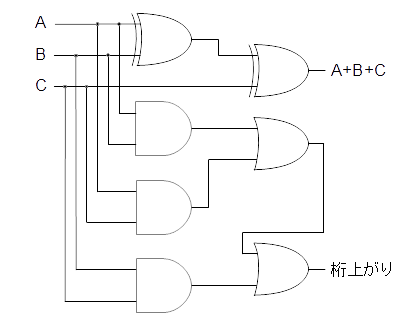
では、実際に8ビットの論理積の例を見てみましょう。01101101と、11110000のAND演算を行ってみます。複数の桁がある場合は、対応けた同士でそれぞれAND演算を行います。その結果、得られる答えは01100000となります。(図6-1.)
全加算回路の3つの入力とその演算結果は、以下の表(表7-2.)のようになります。Cは下位けたからの桁上がりです。
表7-2.全加算器の演算| A | B | C | A+B+C | 桁上がり |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
その他の算術演算
加算以外の算術演算(減算、乗算、除算)も、論理回路の処理の組み合わせで表現できます。まず、減算ですが、2日目で説明したとおり、補数を使うことで負の数を表すので,補数の加算で減算を実現できます。
さらに、乗算は加算を繰り返すことで実現できます。例えば、2×4は,2を4回加算すれば結果を得られます。同様に除算は減算の繰り返しで実現可能で、例えば,10÷2は,10から2が何回引けるかをカウントすることにより得られます。これで,四則演算すべてが論理演算で実現できることがわかります。









