浮動小数点
有限の桁しか扱えないコンピュータの小数
2進数で小数をあつかう場合、もしくは小数を2進数で扱う方法は4日目で紹介したとおりです。しかし、実際にコンピュータで2進数を表現するには、桁数の上限などの様々な制約があります。
そのため、コンピュータで小数を表すためには、浮動小数形式(ふどうしょうすうてんすうけいしき)と呼ばれる方法を用いています。これは、IEEE(アイ・トリプル・イー,Institute of Electrical and Electronics Engineers:米国電気電子技術者協会)で定められている正式な方法です。そこで、ここではコンピュータ内部で浮動小数点がどのようにして扱われているのかについて説明します。
固定小数形式
浮動小数点について説明する前に、まずは固定小数点と呼ばれる方式について説明します。固定小数点とは、すでに説明した2進数の方法で小数を表現する方法です。2進数のある位置を小数点と定め、限られた範囲のビット数で2進数の実数を表現する方法です。たとえば、以下(図5-1.)の法歩だと、0110.1101という2進数は6.8125となります。
図5-1.固定小数点による小数の表現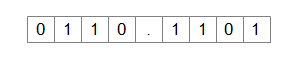
この方法は非常にわかりやすいのですが、一つ大きな問題があります。それは、扱える数の範囲が限られているということです。この場合、整数部分・小数部分がが16通りしか表現できないため、あまり大きな範囲の数値をあつかうことができます。
浮動小数点の考え方
そういった固定小数点の問題を克服するために考案されたのが、浮動小数点方式です。浮動小数点は小数点が移動する方式で、これにより幅広い範囲の数値を表すことが可能になります。具体的に2進数での浮動小数点について説明する前に、まずは10進数でその考え方を理解してみましょう。(図5-2.)
図の左端に表現したい数字です。この数字をまず、+0.1234に10の何乗かの数値がかけられています。これにより、整数と小数の組み合わせができます。この10nという表現部分のことを、これを、符号、小数部分(仮数部)、および10にかける数(指数部)、という組み合わせに変えます。
ただ、このままだと指数部が負になるケースが出てくるので、指数部に負の数の最大値である5を足すことによって正の数だけの表示に変えます。これをバイアス表示と言います。
図5-2.10進数による浮動小数点の考え方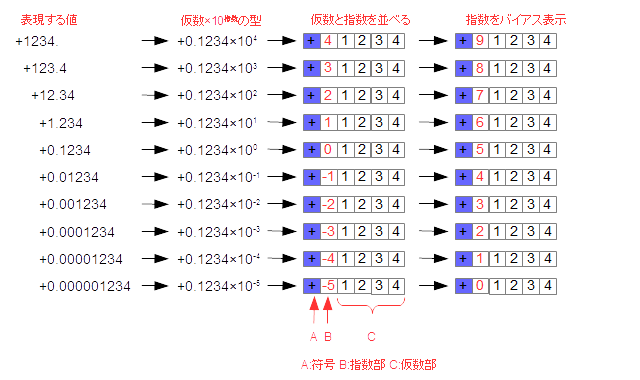
浮動小数点とは、このような考え方です。それにより、この数値は整数としては+99999から-99999まで、小数だと+0.99999から-0.99999まで表現できます。(図5-3.)
図5-3.浮動小数点であらわされる数の範囲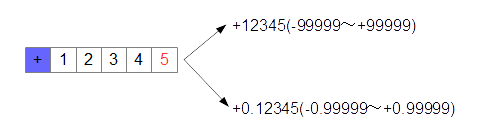
コンピュータ内での実際の浮動小数点の計算は、これを2進数におきかえてものです。
浮動小数点
では、実際に2進数の浮動小数点の表現を見てみましょう。以下の図(図5-4.)を見てください。
図5-4.浮動小数点の形式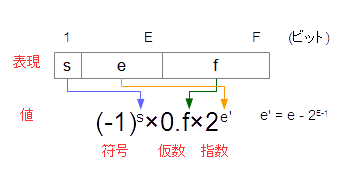
先頭のビット(s)は、符号を表します。また、eは指数部分と呼ばれ、仮数fが小数部分を表し、それらの積によって数値を表します。符号sに1ビット、指数eにEビット、仮数fにFビットを用います。
sが0の場合は正の数、1の場合は負の数を表します。これは、(-1)0=0であり、(-1)-1=-1であることから、符号は(-1)sにまとめられます。
また、指数部分は、バイアス表示が必要となり、e-2E-1をe'として、これをもとに指数の表現に変えます。仮数部fは、先頭に小数点を固定した正の固定小数点であり、その値は、0.fと表します。
このように、制約のあるビット長の中で有効桁数をできるだけ大きくくするためには、仮数はできるだけ左詰めにします。つまり、仮数の先頭が0であれば、指数部の値で調節可能な限り左に寄せます。この操作のことを、正規化と言います。
実際の計算例
では実際に、16ビットの浮動小数点形式の例を見てみましょう。ここでは、以下の図(図5-5.)のようにE=5、F=10である、ビットの列が0100101010000000を実際に見てみましょう。
図5-5.16ビットの浮動小数点形式
この数値を符号、仮数、指数の部分に分解すると、0 10010 1010000000となります。s=0なので、表す数は正の数であり、E=5であることから、バイアスは25-1=16で、あり、eの値は10010、つまり18であることから、e'=18 - 5 = 2となります。
続いて、fの表す部分は0.1010000000なので、これを10進数に直すと0.625となります。したがって、表現する値は、+0.625×22=+2.5となります。
IEEE浮動小数点形式
実際に用いられている浮動小数点方式
続いて、実際にコンピュータ内で用いられているIEEE浮動小数点形式について説明します。この企画には、32ビットと64ビットの2種類があり、それぞれ表現できる範囲が決まっています。(図5-6.)
図5-6.IEEE浮動小数点方式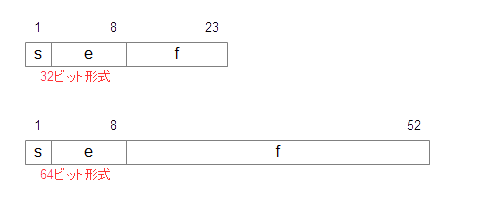
この表現は、C言語では、floatおよびdoubleとして利用されています。C言語のfloatおよび、doubleの範囲は以下のようになります。(表5-1.)C言語に限らず、主要な言語では同じ形式を用いて浮動小数点を表現しています。
表5-1.C言語の主要な基本データ型| データ型 | 呼称 | ビット数 | 範囲 |
|---|---|---|---|
| float | 単精度実浮動小数点型 | 32 | 1.175494351e-38~3.402823466e+38 |
| double | 倍精度実浮動小数点型 | 64 | 2.2250738585072014e-308~1.7976931348623158e+308 |









